Soddy Spiral

Problem: Give an explicit, closed formula for an infinite sequence of distinct circles, each tangent to the previous three as well as the succeeding three.

We could start with three otherwise arbitrary mutually tangent circles, and iterate Soddy's fourth kisser formula forwards and backwards. But the nth iterate of this process is not obvious, nor is the requisite sequence of centers.

But there is one family of Soddy iterates centered on a log spiral, with radii in geometric progression.

load("c:\\rwg\\climax\\sodspiral.lsp")$

c:\rwg\climax\sodspiral.lsp being loaded.

Define the algebraic parameter

(c16) beta=sqrt(2*%i-1)-%i-1

(d16)               beta = sqrt(2 %i - 1) - %i - 1

Then the n^th radius, -inf < n < inf, is

(c17) abs(beta^n/(1+beta))

                               |    n|
                               |beta |
(d17)                       -------------
                            abs(beta + 1)

(where 1/|beta| ~ 2.890) and the n^th center is

(c18) (1-beta^n)/(1-beta)

                                      n
                              1 - beta
(d18)                         ---------
                              1 - beta

Graphically testing,

(c7) dfloat(makelist(realpart(''(subst(d16,d18)))+''(subst(d16,d17)*cos(t)),n,-1,6))

(d7) [2.14711950238564d0 * cos(t) + 1.78615137775742d0,
0.74293413587832d0 * cos(t), 0.25706586412168d0 * cos(t) + 1.0d0,
0.08894847511414d0 * cos(t) + 0.78615137775742d0,
0.03077744784266d0 * cos(t) + 0.7578879212707d0,
0.01064943827864d0 * cos(t) + 0.79557934740074d0,
0.00368485834922d0 * cos(t) + 0.78284269671802d0,
0.00127501382688d0 * cos(t) + 0.78377748633802d0]

(c8) dfloat(makelist(imagpart(''(subst(d16,d18)))+''(subst(d16,d18)*sin(t)),n,-1,6))

(d8) [2.14711950238564d0 * sin(t) + 2.27201964951406d0,
0.74293413587832d0 * sin(t), 0.25706586412168d0 * sin(t),
0.08894847511414d0 * sin(t) + 0.27201964951406d0,
0.03077744784266d0 * sin(t) + 0.15567759497108d0,
0.01064943827864d0 * sin(t) + 0.1728689675164d0,
0.00368485834922d0 * sin(t) + 0.1794454247087d0,
0.00127501382688d0 * sin(t) + 0.1745744391442d0]

(c10) block([plotnum:3*plotnum],paramplot(d7,d8,t,0,2*%pi))$

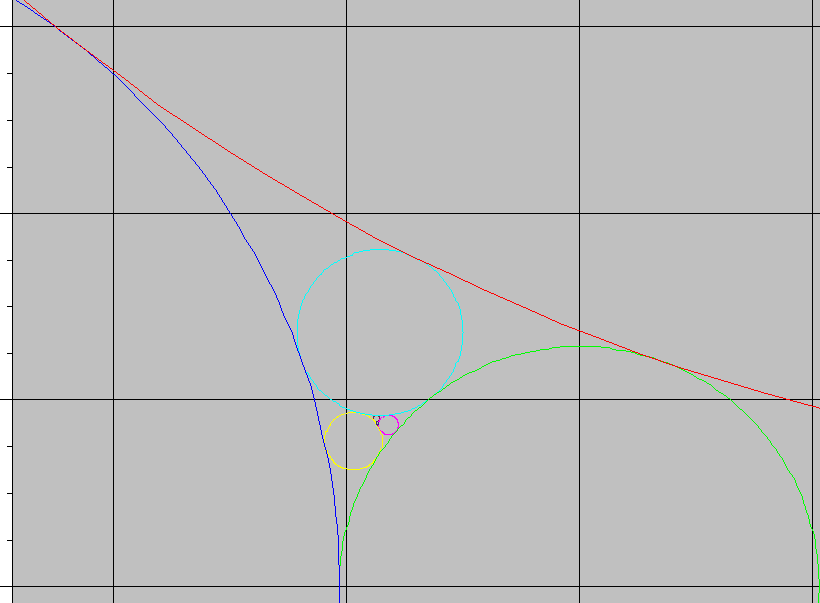
We can then homographically transform this into a three (six?) dimensional continuum of solutions. Many of these solutions will be (circularly) bounded with two accumulation points insead of one.

Possibly there is an inversion in a circle, centered at the 1/(1- b) accumulation point, which reverses the sequence.

(c15) fancy_display:false$